Modern Graduate
Electromagnetics Education—A New Perspective[1]
W.C. Chew
Director, Center for Computational EM and EM Lab.
Department of Electrical and Computer Engineering
University of Illinois
Urbana, IL 61801-2991
ABSTRACT
Electromagnetics is a branch of applied physics that has evolved over the years. The physics associated with electromagnetics is well understood, but despite the age-old advent of Maxwell theory, electromagnetic engineers are indispensable. The primary reason is the pervasiveness of electromagnetic technology in the modern world, where electromagnetic engineers are needed to design systems related to electromagnetic technology, such as in wireless communications, computer chips, optical networks, etc.
Because of the elusiveness of electromagnetic physics and the complexity of the law that governs it, electromagnetic analysis has always been used in the understanding and design of electromagnetic related systems. As a result, electromagnetic analysis is a continuously evolving science, and an important topic of research up to this day, and recently is an important research topic in computational science.
Over the years, electromagnetic analysis has evolved from the solving for scattering solutions from simple shapes, to approximate and perturbation methods, and then more recently, to the use of numerical and fast methods with the help of digital computers.
Electromagnetic analysis is an active area of research that has attracted the interest of mathematicians, computer scientists and engineers. However, a good understanding of modern electromagnetic analysis requires the melange of a deep insight in electromagnetic physics and ability for mathematical finesse, and knowledge of computational numerical algorithms. Therefore, it is naturally an interdisciplinary field.
Due to the advent of fast algorithms for them, electromagnetic simulations will become an indispensable analysis tool in the arsenal of an electromagnetic engineer. She will be involved with design work where simulation tools will be used repeatedly until she arrives at a satisfactory design. The final test of the pudding will still be in the laboratory where the design is built and tested.
While university research emphasizes computational electromagnetics, we have to be mindful that a student of electromagnetics should understand the underlying physics, and develop the requisite physical and engineering intuition and insight for problem solving. These skills are important both for analysis and design. Therefore, it is still important to educate graduate students on the classical electromagnetic analysis methods. For instance, classical electromagnetic analysis teaches us the concepts of surface waves, creeping waves, lateral waves, Goubaud waves, guided modes, evanescent modes, radiation modes, leaky modes, low-frequency physics, and high-frequency physics that do not emerge from numerical analysis, but such concepts are instrumental in a good physical understanding of many electromagnetic interactions.
In terms of mathematical knowledge, classical analysis methods require students to understand harmonic analysis, complex variables, perturbation and asymptotic methods. However, modern numerical approach to problem solving requires students to understand linear algebra and linear vector spaces. At a more advanced level, students will need to understand functional analysis, algebra, and even topology.
In quantum mechanics, one sees a marriage between functional analysis and physics. The physics in quantum mechanics evolved from wave physics, and for a while, was called wave mechanics. However, in electromagnetics, we also see the use of functional analysis ideas in numerical methods such as Galerkin’s method, method of moments, and finite element method.
As
topological concepts found in differential forms become more matured, they will
be important for graduate electromagnetic education as well. For instance, the understanding that Stokes’
theorem and Gauss’ theorem are essentially the same concept topologically, and
similarly for other vector identities in vector calculus, are beautiful
concepts that an electromagnetic graduate student should know.
Introduction
Electromagnetic
theory was fully formulated by James Clerk Maxwell in 1864 in terms of the
Maxwell’s equations. Even though it has
been around for over a hundred years, scientists and engineers are continuously
pursuing new methods to solve these equations. The reason is that Maxwell’s equations govern the law for the
manipulation of electricity. Hence, many
branches of electrical engineering are directly or indirectly related to the
electromagnetic theory. Scientists and
engineers solve these equations in order to gain a better understanding of and
physical insight into systems related to the use of electromagnetic fields and
waves. The solutions of Maxwell’s
equations can also be used to predict design and experimental outcomes.
Electromagnetics
has persisted as a vibrant field despite it being over a hundred year old is
because many electrical engineering technologies depend on it. To name a few, these are: physics based
signal processing and imaging, computer chip design and circuits, lasers and
optoelectronics, MEMS (micro-electromechanical sensors) and microwave
engineering, remote sensing and subsurface sensing and NDE (non-destructive
evaluation), EMC/EMI (electromagnetic compatibility/electromagnetic
interference) analysis, antenna analysis and design, RCS (radar cross section)
analysis and design, ATR (automatic target recognition) and stealth technology,
wireless communication and propagation, and biomedical engineering and biotech.
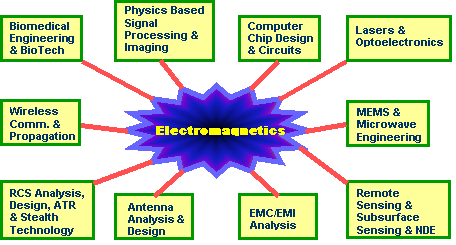
Figure 1. The impact of electromagnetics is far-reaching and affects many different branches of electrical engineering technologies.
For instance,
the field of computer chip design has long relied on the use of circuit theory,
which is a subset or an approximation of electromagnetic theory when the
frequency is very low. As the clock
frequency of a computer becomes higher, circuit theory becomes inadequate in
describing many of the physical phenomena that occurs within a computer
chip. Electromagnetic theory has to be
used to correctly describe the physics within a computer chip. An emerging electromagnetic analysis method
is computational electromagnetics where the computer is used intensively to
analyze electromagnetic problems. The
growth of this field has been spurred by the rapid growth of computer speed,
and now the further growth and design of faster computers will rely on
computational electromagnetics—a symbiotic existence indeed.
A Brief Incomplete History of Analysis with Maxwell’s Theory
Electromagnetics,
the study of the solution methods to solving Maxwell’s equations, and the
application of such solutions for understanding and engendering new
technologies, has a long history of over a hundred years. But the analysis method with Maxwell’s
equation is constantly evolving over the years. In the beginning, there was the age of simple shapes: during this
period, roughly between the late 19th century to 1950s, solution
methods, such as the separation of variables, harmonic analysis, and Fourier
transform methods were developed to solve for the scattering solution from
simple shapes. We can identify the
names of Sommerfeld, Rayleigh, Mie, Debye, Chu, Stratton, Marcuvitz, and Wait
for contributions during this era. Many
of the solutions are documented in a book by Bowman, Senior and Uslenghi.
Despite
the successful closed form solution of many simple geometries, the solutions
available were insufficient to analyze many electromagnetic systems. Hence, scientists and engineers started to
seek approximation solutions to Maxwell’s equations. This was the age of approximations, roughly between 1950s and
1970s. During this period, asymptotic
and perturbation methods were developed to solve Maxwell’s equations. The class of solvable problems for which
approximate solutions exist, was greatly enlarged. We can identify names such as Bremmer, Keller, Jones, Kline,
Fock, Hansen, Lee, Deschamps, Felsen, and Marcuvitz during this era.
However,
the limited range of approximate solutions of Maxwell’s theory still could not
meet the demand of many engineering and system designs. As soon as the computer was developed,
numerical methods were studied to solve Maxwell’s equations. This was the age of numerical methods
(1960s+). Method of moments (MOM),
finite difference time domain method (FDTD), and finite element method (FEM)
were developed to solve problems alongside with many other numerical
methods. In particular, Harrington was
noted for popularizing MOM among the electromagnetics community, while it is
know as the boundary element method (BEM) in other communities. Yee developed FDTD, for solving Maxwell’s
equation. Finite element has been with
the structure and mechanics community, and Silvester was an early worker who
brought its use into the electromagnetics community. Other names commonly cited in this field are: Wilton, Mittra,
and Taflove.
There
has always been marriage between electromagnetics and mathematics from the very
beginning—a marriage made in heaven perhaps.
Actually, quite sophisticated mathematical techniques were used to
analyze electromagnetic problems because electromagnetic theory was predated by
the theory of fluid and theory of sound.
These fields were richly entwined with mathematics with the work of
famous mathematicians such as Euler, Lagrange, Stokes, and Gauss. Moreover, many of the mathematics of
low-Reynold number flow in fluid theory and scalar wave theory of sound can be
transplanted with embellishment to solve electromagnetic problems.
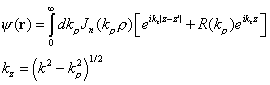
Examples of problems solved during
the age of simple shapes are the Mie and Debye scattering by a sphere and
Rayleigh scattering by small particles.
Rayleigh also solved the circular waveguide problem for electromagnetic
waves because he was well versed in the mathematical theory of sound, having
written three volumes on the subject while sailing down the Nile River. Sommerfeld solved the half plane problem as
far back as 1896 because the advanced mathematical techniques were available
then. He also solved the Sommerfeld
half space problem in 1949 in order to understand the propagation of radio
waves over the lossy half-earth. The
problem was solved in terms of, what is now known as, the Sommerfeld integrals,
an example of which is as follows:

Figure 2. A dipole over a half space. The problem was first solved by Sommerfeld to understand the propagation of radio waves over the lossy earth.
Evaluating
the Sommerfeld integrals was an impossibility during his time, but it is a
piece of cake now in the modern era.
Subsequently, approximation techniques, such as the stationary phase
method, the method of steepest descent, and the saddle point methods were used
to derive approximations to the Sommerfeld integrals.
However,
even though electromagnetics has been intimately entangled with mathematics, a
student of electromagnetics has to be able to read the physics into the mathematical
expressions that describe the solutions of Maxwell’s equations. Approximate methods generally help to
elucidate the physics of the wave interaction with complex geometry.
The
physical insights offered by approximate solutions spurred the age of
approximations, roughly between 1950s and 1970s. A large parameter such as frequency is used to derive asymptotic
approximations. Moreover, heuristic
ideas were used to derive the physical optics approximation, Kirchhoff
approximation, and various geometrical optics approximations. These approximations eventually lead to the
geometrical theory of diffraction and the uniform asymptotic theory of
diffraction. The applications of these
approximate methods to scattering by complex structures are usually ansatz
based. The ansatz assumes that the
scattering solution is of the form:
![]()
The leading coefficient ![]() and the exponent
and the exponent ![]() are found from canonical solutions such as the Sommerfeld
half plane problem, or scattering by a sphere or a cylinder, followed by the
use of Watson transformation. The use
of approximate solution enlarges the class of solvable problems, but the error
is usually not controllable. Asymptotic
series are semi-convergent series; hence there is not a systematic way to
reduce the solution error by including more terms in the ansatz. Moreover, the range of application is
limited because the frequency has to be sufficiently high before the ansatz forms
a good approximation.
are found from canonical solutions such as the Sommerfeld
half plane problem, or scattering by a sphere or a cylinder, followed by the
use of Watson transformation. The use
of approximate solution enlarges the class of solvable problems, but the error
is usually not controllable. Asymptotic
series are semi-convergent series; hence there is not a systematic way to
reduce the solution error by including more terms in the ansatz. Moreover, the range of application is
limited because the frequency has to be sufficiently high before the ansatz forms
a good approximation.
The
advent of the transistorized computer in the 1960s almost immediately brought
about the birth of numerical methods for electromagnetics. The method of moments (MOM) was popularized
among the electromagnetics community by Harrington in the 1960s. The method is integral-equation-based, and
is versatile for solving problems with arbitrary geometries. It entails a small number of unknowns since
the unknown is the current, but unfortunately, the pertinent matrix equation is
dense. The finite-difference
time-domain method was proposed by Yee in the 1960s for solving Maxwell’s
equations in its partial differential form.
The method is extremely simple, and gives rise to a sparse matrix
system. Since the field is the unknown
to be solved for, the drawback is that it entails a large number of
unknowns. Moreover, the field is always
propagated from point to point via a numerical grid, hence yielding grid
dispersion error, which accentuates with increasing problem size.
However,
some of the recent advances in fast computational algorithms will remove the
objections to the shortcomings of numerical methods.
Roles of Physics, Mathematics, and Computer Science in Electromagnetics
Physics Knowledge
Electromagnetics
is a branch of applied physics.
However, due to the dependency of solution methods on mathematics, both
knowledge of physics and mathematics are indispensable in the study of
electromagnetics.
We
should encourage our students to study modern physics; even though it is not
directly relevant to electromagnetics, modern physics embodies the most
beautiful of the physical theories that have been developed in this
century. If a student can understand
the thought processes and abstraction that go on in modern physics, she
eventually will become a better thinker and a proficient problem solver. Our goal is to teach a student to think in
graduate school. A proverbial saying is
that “If you give a man a fish, it lasts him for a day, but if you teach a man
how to fish, it lasts him a lifetime.”
Moreover, if we can stretch the mind of a student, it does not regain
its original dimension.
The
long history of electromagnetics has produced much classical knowledge that
cannot be ignored by our students. They
should have a good understanding of the fundamental solutions that accompany
simple shapes. Furthermore, they should
understand and should be able to elucidate the physics that arises from the
approximate solutions, such as the physics of surface waves, creeping waves,
lateral waves, Goubaud waves, evanescent waves (tunneling), guided modes,
radiation modes, leaky modes, specular reflection, edge diffraction etc.
A
student of electromagnetics should be cognizant of the metamorphosis of the
physics over different lengthscales or frequencies. When the wavelength is extremely long, one is in the regime of
electrostatics and magnetostatics where the electric field and the magnetic
field are decoupled or weakly coupled to each other. This is also the world in which circuit theory lives in. For shorter wavelengths, the coupling between
the electric and magnetic field becomes stronger, and we have mid-frequency or
high frequency electromagnetics, whose physics is quite different from low
frequency electromagnetics. This is
also when the wave nature of an electromagnetic field becomes important. Often, the vector nature of electromagnetic
field plays an important role in this regime.
As the frequency gets higher, then we are in the world of optics and ray
optics. In this world, electromagnetic
waves can be described by rays, and often be thought of as particles. Equations can be derived to govern only the
propagation of the envelop of a pulse.
At very high frequencies, the quantization of the energy associated with
an electromagnetic field becomes important.
A quantum of energy in electromagnetic field is ![]() where the Planck
constant
where the Planck
constant ![]() erg sec. Therefore,
to properly understand the interaction of very high frequency electromagnetic
field with material, we have to invoke quantum electrodynamics.
erg sec. Therefore,
to properly understand the interaction of very high frequency electromagnetic
field with material, we have to invoke quantum electrodynamics.
Mathematics Knowledge
Since
there has often been an intimate intermarriage between electromagnetics and
mathematics, a student of electromagnetics should understand the reason for the
finesse, care, and precautions that mathematicians go through in their
work. It is to lay a firm foundation
for their mathematical work so that others can build upon them. She should understand the fundamental of
harmonic analysis and complex variables, which traditionally have been used to
analyze classical electromagnetic problems.
The fundamental of perturbation and asymptotic methods should be
understood in order to appreciate the wide body of knowledge generated by
approximate calculations.
The
advent of computational electromagnetics however, calls for the use of a
different body of mathematical knowledge.
A student who is well versed in computational electromagnetics should
have an elementary understanding of functional analysis, Hilbert spaces, and
operator theory. She should also
understand partial differential equation (PDE) theory, the existence,
uniqueness, and well-posedness of PDE solutions, and the integral equation
theory that follows from PDE. A
wonderful aspect of modern computational electromagnetics is the error
controllability of the solution—viz., the error can be made increasingly small
by devoting increasing computational resources. Hence, the pervasiveness of computational method in the future
will require that a student understands the elements of approximation theory
and error bounds.
My
students, F. Teixeira and E. Forgy have convinced me that often times, a more
elegant view of electromagnetic theory can be gotten from a topological
viewpoint. Such is the viewpoint of
electromagnetic theory from differential forms. Modern computational electromagnetics will inherently deal with
complex geometry handling. A more
profound understanding of electromagnetic theory through a topological
viewpoint may even engender the development of new numerical methods.
Computer Science
Computers
are used by all scientists and engineers as a tool. In order to harness the power of this tool effectively, it is
important that a student of electromagnetics understands the basics of modern
computer languages and computer architectures. A student should understand the basis of object oriented
programming paradigm, and how its use will result in better computer code
maintenance, reusability, and encapsulation.
It is also important for students to learn the basis of parallel
computing and large scale computing, and the need to use message passing for
distributed processor computing. Many
fast algorithms exist in computer science for sorting, searching, matrix
manipulations that students should be aware of. They should also be aware of the element of computer
architecture, the issue of distributed memory computing versus shared memory
computing, the issue of memory latency, cache usage, cache hit and miss. Geometry handling will be indispensable from
computational electromagnetics; hence, a student should understand certain
aspects of computational geometry.
Types of Graduate Students
It is
important that one educates independent thinkers rather than just high-class
technicians who are automatons good at receiving and executing
instructions. After being a professor
for so many years, I can roughly classified students into three types:
I. Students who will do A when instructed to do A.
II. Students who will do A+B when instructed to do A.
III. Students who will do C when instructed to do A.
Type I
students are what we call high-class technicians. If a professor has many of them, they will help expand the
capabilities of a professor. However,
it is the Type II student who will truly empower and amplify the capabilities
of a professor, and provide work beyond the call of duty. Just imagine how much more productive our
workforce will be if all our students are of Type II. Type III students are an interesting class. They may be either extremely creative or
unproductive. They may also be students
who like to take on a completely different path and break new grounds. So while professors may not be comfortable
with them, they should be allowed to thrive if there is inkling that they are
doing some good. It is important that
we allow people to go outside a beaten path and explore new grounds.
How Do We Stimulate Creativity?
We should always seek to bring the best people into our field and stimulate their creativity. Good people will always bring new ideas, forge new frontiers, and create new areas to work on.[2] We should also cultivate independent thinking in our students. Students should be encouraged to challenge the thinking of a professor. If we force our students to blindly follow the instructions of a professor, it will no doubt stifle the creativity of a student. There is an old Chinese adage:
“If one
believes completely in the teacher, it’s better not to have teachers; if one
believes completely in books, it’s better not to have books.”
There
should be a constant dialogue between professors and students. These dialogues provide a window into the
mind of the student, and provide a venue to link minds. Modern technology and scientific problems
are getting increasing sophisticated that many of them cannot be solved by just
a single mind. Teamwork and linking of
minds are important for the solutions to many of our advanced technological and
scientific problems.
It
is well known that our right brain is responsible for creative and artistic
expressions, and that our left brain is for logical thinking. Students should not precipitate an early
burnout by being one-dimensional and working only with their left-brain. They should be encouraged to pursue the
appreciation of the arts, music and sports to maintain a healthy mind. A student with a healthy mind will
eventually be more creative than a mentally exhausted one.
Roles of Graduate Students in Academe and Industry
When
educating students, we have to be aware that students often time, play a very
different role in the academe as oppose to the industry. In the university, we are pushing the
frontiers of knowledge, and our prerogatives are quite different. In the industry, a student is often involved
with the development or improvement of a technology. Therefore, when educating students, we should be mindful that
students would not work on the kind of problems they work on while they were
graduate students.
In
the academe, since the current hot area of research is electromagnetic analysis
using computational electromagnetics, many universities are doing software
research related to computational electromagnetics. A student typically studies and develops algorithms and
methodologies for computational electromagnetics. Some may even apply these methodologies to some
applications. Often times, these
students are heavily involved with computer programming.
In
another scenario, a student may learn how to build a component of a larger
system. She may be using existing CAD
tools to design a component for her research goals.
However,
when a student graduates, she will most likely be a system or component design
engineer, who helps develop the next generation electromagnetics
technology. The work is very different
from her graduate schoolwork.
Therefore, it is imperative that we teach our students to be thinkers
rather than high-class technicians. It
is instrumental that the students understand the physics of electromagnetics in
graduate schools. Understanding the
physics deeply means the understanding of the mechanism behind how things
work. Therefore, an EM graduate student
has a tall calling, but an exciting one involving a lifetime of learning.
Conclusions
Since
electromagnetic analysis has been used as a prediction tool important for many
branches of electrical engineering, electromagnetics will always remain
important in electrical engineering technologies. However, the long and rich history of electromagnetics offers us
a challenge on how we should educate our graduate students in this rapidly
changing world. The total amount of
knowledge cannot be taught to all our students within the short span of their
graduate education. The important
knowledge changes with changing times.
Therefore, it is extremely important that we educate our students with
the fundamental knowledge, so that she can read further independently if it
needs be. Learning everything relevant
to electromagnetics technology will entail a lifetime of learning. Also, it is important that we educate our
students to become thinkers rather than one who regurgitates our knowledge
mechanically. Furthermore, if we can
educate a student who can empower an organization, the student will undoubtedly
be more valuable to the society.
Since
the role of a student changes from the university to the industry, it is
important that students develop physical insight into their work as graduate
students, so that they will become better system and design engineers in the
industry. They will also become better
problem solvers with better physical insight.
It
is important that we bring the best and brightest, and the most creative people
to work in our field. These new people
will always create new frontier problems to work on. Consequently, there is no shortage of problems to work on and the
field of electromagnetics will be constantly rejuvenated.